To support inheritance Scala has introduced a concept called trait, almost similar to Java Interfaces. But unlike Java Interfaces, Scala traits can actually define any concrete method. From this, it seems apparently that Scala supports multiple inheritance, but that is not the case. To avoid multiple inheritance Scala uses a technique called linearization to flatten calls to super classes.

To illustrate this linearization technique we will use some Scala classes mixed in with Scala Traits as shown in the inheritance structure below:

 

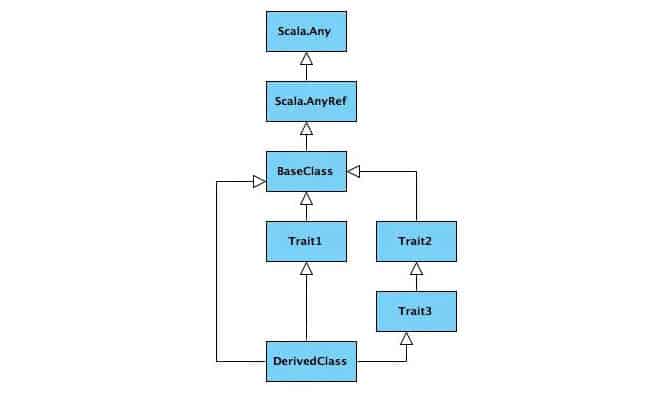
Now, say, BaseClass has a function print and each of the traits as well as the DerivedClass overrides the print function and also calls the print function of the super class. So the class/trait definitions are as follows:

 

So the question is if we call the print function of the DerivedClass what will be the call flow of the print function of the superclasses? (Please note that each of the overridden functions in each class/trait has a call to the print function of the superclass)

Had Scala supported multiple inheritance, the above calls would have created an ambiguity as one cannot be sure which of the print functions would get called, or even whether the print function of the base class would get called thrice. But Scala avoids this ambiguity by linearization.

Scala Linearization technique uses the following equation to flatten the calls to the superclasses and avoid multiple inheritance (Reference Scala Language Specification Section 5.1.2):

 

Where +: denotes a concatenation function where elements at the right-hand operand replace identical elements of the left-hand operand as follows:

 

Also C1… Cn denotes the inherited classes/traits in the order that they are declared for the class from left to right.

We will use our sample class hierarchy to explain the above linearization equation.

If we want to find out the linearization structure of DerivedClass defined as

 

then the above parameters of linearization for this derived class would be:

 

Then the linearization equation for the derived class will be:

 

Now we will apply the same equation for all other classes and traits.

So, for BaseClass the definition is

 

Thus the linearization equation of BaseClass would be

 

(NOTE: Though we did not add any superclass of BaseClass, as per Scala hierarchy the default superclass of any Scala class is scala.AnyRef, similarly scala.AnyRef extends scala. Any)

Simplifying, we will get the following:

 

Applying the same equation for Trait1 which is defined as:

 

the linear form will be:

 

Similarly for Trait2 and Trait3 we get:

 

And

 

So we get the following linear form of all the classes/traits:

 

Except for the derived class, all other classes/traits have the linear form. Let us now use the equation to linearize the DerivedClass

 

If we simplify the above equation and apply the `+:` operation we get the following equation:

 

Just to explain the above simplification logic we are using the +: operation which is defined as

 

So far,

 

the “BaseClass, scala.AnyRef, scala. Any” of the left operand is removed since the right operand also has the same and the result is

 

So the final linear form of the DerivedClass is:

(DerivedClass, Trait3, Trait2, Trait1, BaseClass, scala.AnyRef, scala.Any)

If we call the print function of the DerivedClass we will get the following output:

 

This proves that when we call the print function of the DerivedClass each of the classes/traits has a call to super. print, the call will follow the above linear sequence and thus Scala avoids multiple inheritance.

The following diagram shows the inheritance and the linearization for our sample classes/traits:

 

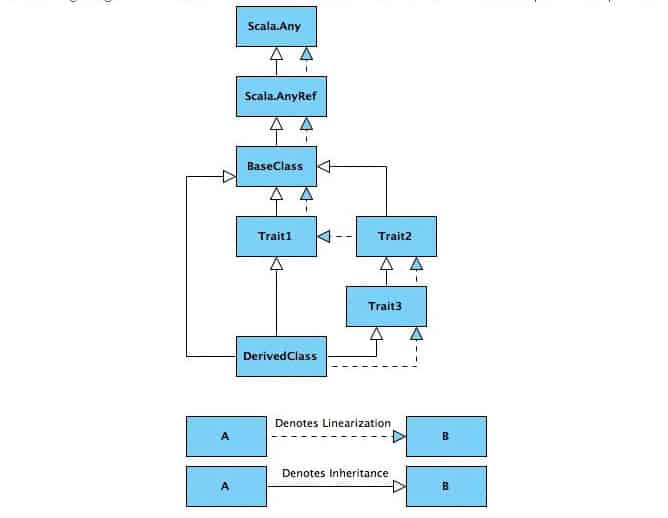
The linear form of a class hierarchy will depend on the order of the traits imported. For example, if we change the definition of our DerivedClass from

 

to

 

and then apply the above series of equations, we will get a different linear form of our DerivedClass which will be:

 

So, the conclusion is that the definition of a trait does not define the linear form, instead how it is mixed in with a class defines the actual linear form.

Author: Dipta P. Banerjee